Cython implementation of calculating halo regions for periodic boundaries
For analysing molecular dynamics results, it’s common to have to take care of periodic boundary conditions as demonstrated by Thor:
I wanted to play around with some different algorithms for calculating distances (KDTrees, Octrees etc) however many of these can’t natively handle periodic boundaries, and it’s not immediately clear to me if they even can handle them.. Could I hack a tree structure to wrap around onto itself?
Rather than worry about that, I decided instead to create an “augmented” set of coordinates,
using the function make_halo below.
A slab of thickness r from each of the 6 faces is replicated on the other side of the simulation box.
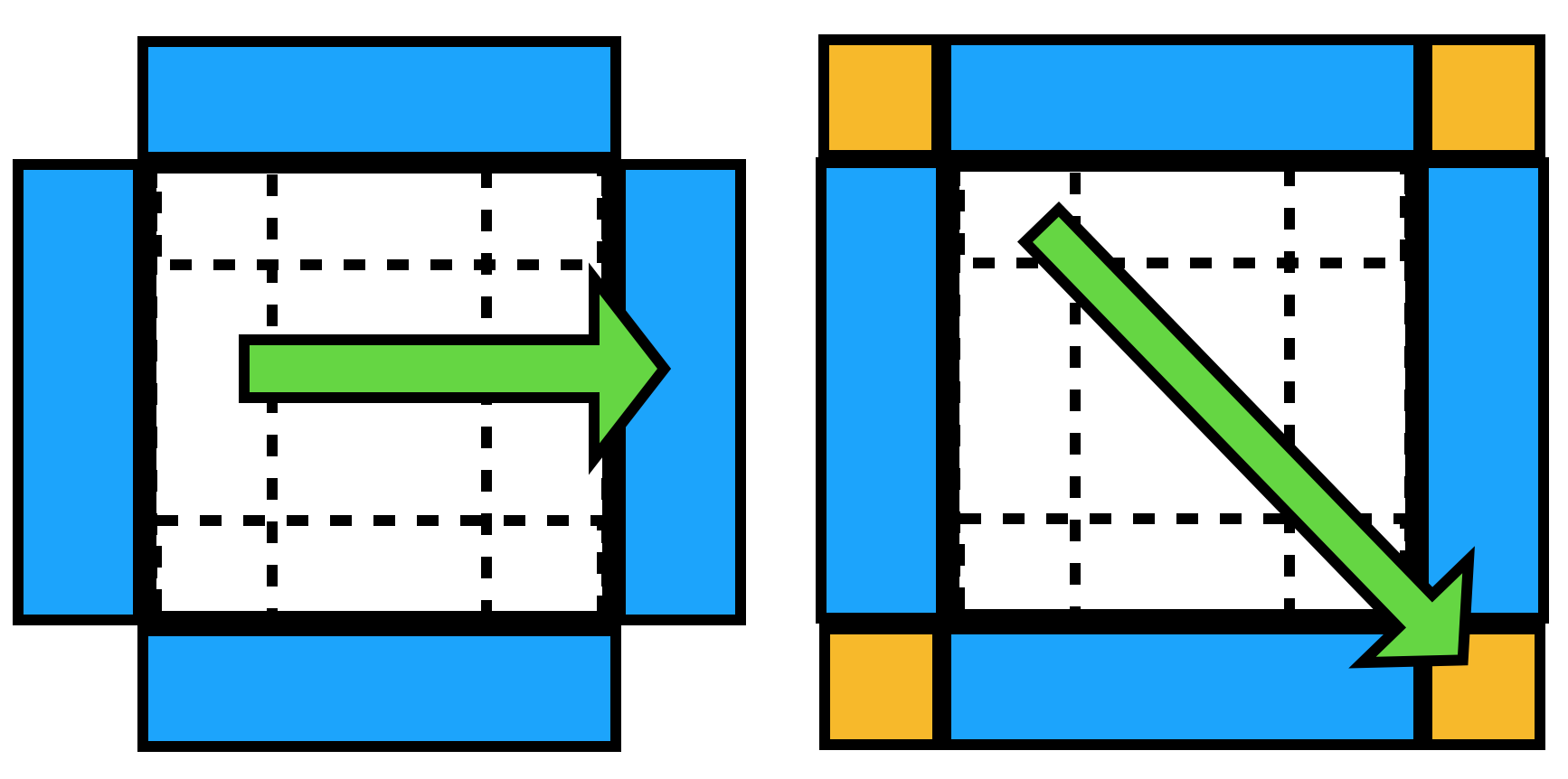
Twelve smaller edge pieces (the intersection of these 6 face slabs, handled by the nested if statements) and eight corner pieces (intersections of intersections, the most nested if statements) are similarly replicated on the opposite side of the simulation volume.
With the coordinates replicated, I can use a “regular” distance calculation algorithm, then later worry about undoing the augmentation…
To completely replicate periodic boundary conditions, the thickness replicated should be half a box length, resulting in a box twice the size of the original. However for many analyses (and with increasing simulation box sizes) the required thickness to replicate is a much smaller fraction of the overall box size.
The undo_augment function then translates indices back down to the original indices. Eg if I started with 100 coordinates, I could then create an augmented set with 110. If I then plugged these into a distance algorithm and got results back about position 105 (or any larger than 100), I know that this actually corresponds to one of the original 100 coordinates.
import scipy.spatial
import numpy as np
%load_ext cython
%%cython
cimport cython
import cython
cimport numpy as np
import numpy as np
@cython.boundscheck(False)
@cython.wraparound(False)
def make_halo(float[:, :] coordinates, float[:] box, float r):
"""Calculate augmented coordinate set
Parameters
----------
coordinates : np.ndarray
coordinates to augment
box : np.ndarray
size of box
r : float
thickness of halo region to buffer by
Returns
-------
augmented : np.ndarray
coordinates of the new augmented coordinates
indices : np.ndarray
original indices of the augmented coordinates
"""
cdef bint lo_x, hi_x, lo_y, hi_y, lo_z, hi_z
cdef int i, j, p, N
cdef float shiftX[3]
cdef float shiftY[3]
cdef float shiftZ[3]
cdef float coord[3]
# room for adding triclinic support by using (3,) vectors
shiftX[0] = box[0]
shiftX[1] = 0.0
shiftX[2] = 0.0
shiftY[0] = 0.0
shiftY[1] = box[1]
shiftY[2] = 0.0
shiftZ[0] = 0.0
shiftZ[1] = 0.0
shiftZ[2] = box[2]
N = coordinates.shape[0]
p = 0 # output counter
# allocate output arrays
# could be more conservative with this
# or use C++ vectors + push etc
cdef float[:, :] output = np.zeros((N, 3), dtype=np.float32)
cdef int[:] indices = np.zeros(N, dtype=np.int32)
for i in range(N):
for j in range(3):
coord[j] = coordinates[i, j]
# detect which face regions particle i is in
lo_x = coord[0] <= r
hi_x = coord[0] >= box[0] - r
lo_y = coord[1] <= r
hi_y = coord[1] >= box[1] - r
lo_z = coord[2] <= r
hi_z = coord[2] >= box[2] - r
if lo_x:
# if X, face piece
for j in range(3):
# add to output
output[p, j] = coord[j] + shiftX[j]
# keep record of which index this augmented position was created from
indices[p] = i
p += 1
if lo_y:
# if X&Y, edge piece
for j in range(3):
output[p, j] = coord[j] + shiftX[j] + shiftY[j]
indices[p] = i
p += 1
if lo_z:
# if X&Y&Z, corner piece
for j in range(3):
output[p, j] = coord[j] + shiftX[j] + shiftY[j] + shiftZ[j]
indices[p] = i
p += 1
elif hi_z:
for j in range(3):
output[p, j] = coord[j] + shiftX[j] + shiftY[j] - shiftZ[j]
indices[p] = i
p += 1
elif hi_y:
for j in range(3):
output[p, j] = coord[j] + shiftX[j] - shiftY[j]
indices[p] = i
p += 1
if lo_z:
for j in range(3):
output[p, j] = coord[j] + shiftX[j] - shiftY[j] + shiftZ[j]
indices[p] = i
p += 1
elif hi_z:
for k in range(3):
output[p, j] = coord[j] + shiftX[j] - shiftY[j] - shiftZ[j]
indices[p] = i
p += 1
if lo_z:
for j in range(3):
output[p, j] = coord[j] + shiftX[j] + shiftZ[j]
indices[p] = i
p += 1
elif hi_z:
for j in range(3):
output[p, j] = coord[j] + shiftX[j] - shiftZ[j]
indices[p] = i
p += 1
elif hi_x:
for j in range(3):
output[p, j] = coord[j] - shiftX[j]
indices[p] = i
p += 1
if lo_y:
for j in range(3):
output[p, j] = coord[j] - shiftX[j] + shiftY[j]
indices[p] = i
p += 1
if lo_z:
for j in range(3):
output[p, j] = coord[j] - shiftX[j] + shiftY[j] + shiftZ[j]
indices[p] = i
p += 1
elif hi_z:
for j in range(3):
output[p, j] = coord[j] - shiftX[j] + shiftY[j] - shiftZ[j]
indices[p] = i
p += 1
elif hi_y:
for j in range(3):
output[p, j] = coord[j] - shiftX[j] - shiftY[j]
indices[p] = i
p += 1
if lo_z:
for j in range(3):
output[p, j] = coord[j] - shiftX[j] - shiftY[j] + shiftZ[j]
indices[p] = i
p += 1
elif hi_z:
for j in range(3):
output[p, j] = coord[j] - shiftX[j] - shiftY[j] - shiftZ[j]
indices[p] = i
p += 1
if lo_z:
for j in range(3):
output[p, j] = coord[j] - shiftX[j] + shiftZ[j]
indices[p] = i
p += 1
elif hi_z:
for j in range(3):
output[p, j] = coord[j] - shiftX[j] - shiftZ[j]
indices[p] = i
p += 1
if lo_y:
for j in range(3):
output[p, j] = coord[j] + shiftY[j]
indices[p] = i
p += 1
if lo_z:
for j in range(3):
output[p, j] = coord[j] + shiftY[j] + shiftZ[j]
indices[p] = i
p += 1
elif hi_z:
for j in range(3):
output[p, j] = coord[j] + shiftY[j] - shiftZ[j]
indices[p] = i
p += 1
elif hi_y:
for j in range(3):
output[p, j] = coord[j] - shiftY[j]
indices[p] = i
p += 1
if lo_z:
for j in range(3):
output[p, j] = coord[j] - shiftY[j] + shiftZ[j]
indices[p] = i
p += 1
elif hi_z:
for j in range(3):
output[p, j] = coord[j] - shiftY[j] - shiftZ[j]
indices[p] = i
p += 1
if lo_z:
for j in range(3):
output[p, j] = coord[j] + shiftZ[j]
indices[p] = i
p += 1
elif hi_z:
for j in range(3):
output[p, j] = coord[j] - shiftZ[j]
indices[p] = i
p += 1
return np.array(output[:p]), np.array(indices[:p])
@cython.boundscheck(False)
@cython.wraparound(False)
def undo_augment(int[:] results, int[:] translation, int nreal):
"""Translate augmented indices back to originals
Note: modifies results in place!
Parameters
----------
results : ndarray of ints
indices of coordinates, including "augmented" indices
translation : ndarray of ints
original indices of augmented coordinates
nreal : int
number of real coordinates, ie values in results equal or larger than this
need to be translated to their real counterpart
Returns
-------
results : ndarray of ints
"""
cdef int N
N = results.shape[0]
for i in range(N):
if results[i] >= nreal:
results[i] = translation[results[i] - nreal]
return results
Cython experience:
I played around with a few different Cython versions of this.
Memoryviews (i.e. float[:, :] coordinates) proved to be much faster than defining the types wrt numpy (ie np.ndarray[np.float32_t, ndim=2]) which matches the benchmarks here.
My original Python version took about 50ms on my test case,
the above Cython version takes 0.1ms, which isn’t really unexpected considering the amount of looping we have to do.
The loops over the three dimensions are ugly (and not very Python), but just using output[p, :] = coord + shiftX gave poor performance.
This was visible using the annotation option (%%cython -a) which highlights where Python calls are made in yellow.
Generally you want to minimise yellow lines, especially in all the loops!
Using these functions
With the augment/undo functions created, I can now wrap different distance calculations which are themselves ignorant to periodic boundary conditions. Here I find all positions which are within 2.0 of each other (ie a rough approximation of guessing molecular bonds).
def kdt_guess_bonds(coordinates, box, r_max):
"""Find all pairs of coordinates within r_max"""
# create augmented coordinates
aug, idx = make_halo(coordinates, box, r_max)
# add these to original coordinates
aug_coord = np.concatenate([coordinates, aug])
# find pairs using scipy.spatial.KDTree
kdtree = scipy.spatial.cKDTree(aug_coord)
pairs = np.array(list(kdtree.query_pairs(r_max)), dtype=np.int32)
# convert indices back to "original" indices
undo_augment(pairs[:, 0], idx, len(coordinates))
undo_augment(pairs[:, 1], idx, len(coordinates))
return pairs
coords = np.random.random((5000, 3)).astype(np.float32) * 30.
box = np.array([30, 30, 30, 90, 90, 90], dtype=np.float32)
kdt_guess_bonds(coords, box, 2.)
array([[ 859, 2464],
[ 943, 3195],
[ 997, 2857],
...,
[2148, 4550],
[ 925, 2237],
[ 284, 760]], dtype=int32)
Future work
The point of these augment/undo wrapper functions is to try and bring my problem towards more possible solutions. Finding nearest neighbours is (hopefully) a solved problem, but maybe this hasn’t been brought to molecular dynamics yet…
